Taxonomic Classification - Kraken

Kraken

Kraken 1

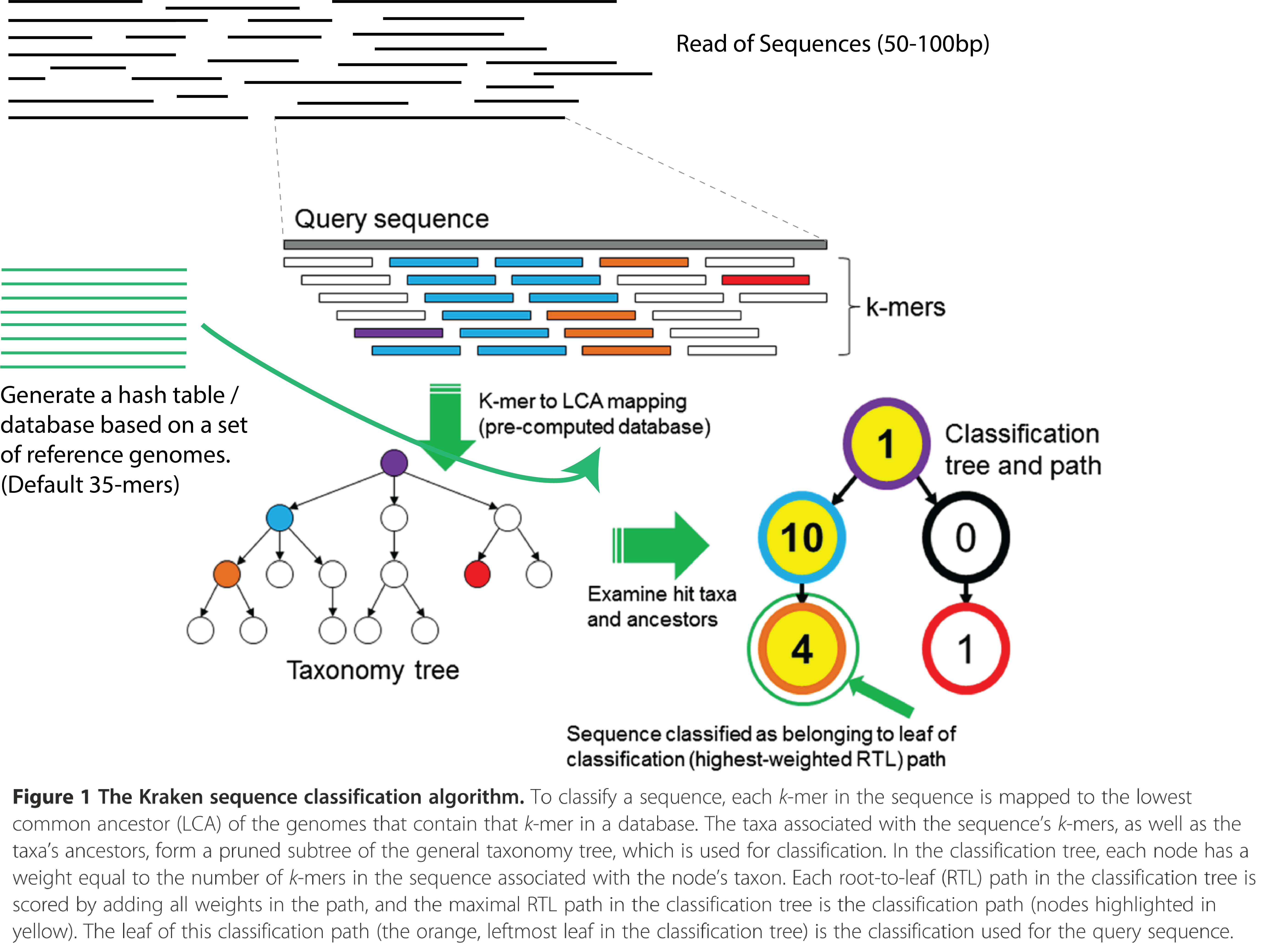
Kraken is a k-mer based taxonomic classifying tool for metagenomic sequencing data. It generates a k-mer hash lookup table from known reference genomes and assigns the lowest common ancestor (LCA) to each k-mer. Given a seqquencing read (S), break down S into a series of k-mers. Instead of aligning sequencing reads to the reference genomes, look up the hash table for an exact match of the k-mers and assign it the respective LCA.

Using the LCA assignments, we create a truncated and weighted phylogenetic profile of the k-mers and look for the root-to-leaf (RTL) path with the highest score. The leaf with the highest RTL score is now assigned to (S). Repeat for all the other S in the library. See diagram below for more details.

“Building the standard Kraken database downloads and uses all complete bacterial, archeal, and viral genomes in Refseq at the time of the build.” To build a standard database, you will need roughly 200GB of space, and a huge RAM to load the hash table. Due to the sheer size of the database, it is unlike that a home computer will be appropriately speced. Instead of making a pre-built hash table available for download, Kraken provides a smaller database (MiniKraken) that can be run on computeres with 16GB or less RAMs.

The defaults are \(k=31\) and \(l=15\).

Kraken 2

Kraken 2 makes several improvements to the hash table, resulting in a very slightly less accurate assignment in return for a faster database build time and smaller memory usage. The key improvements are highlighted below.

“Compact hash table allows Kraken 2 to use 32 bits for a key-value pair, a reduction compared to the 96 bits used by Kraken 1 (64 bits for key, 32 for value) (Figure. 1c). But it also creates a new way in which keys can “collide,” in turn impacting the accuracy of queries to the CHT. Two distinct keys can be treated as identical by the CHT if they share the same compact hash code and their starting search positions are close enough to cause a linear probe to encounter a stored matching compact hash code before an empty cell is found. This property gives the CHT its probabilistic nature, in that two types of false-positive query results are possible: either (a) a key that was not inserted can be re- ported as present in the table or (b) the values of two keys can be confused with each other.”

“Kraken 2 performs hash-based subsampling to reduce the memory requirement of the databases. It estimates the required capacity of the hash table given the k, l, and s values chosen along with the sequence data in a database’s reference genomic library. If the estimated required capacity is larger than the maximum requested size, then the minimizers will be subsampled further using a hash function.

1. Given an estimated required capacity S′ and a maximum user-specified capacity of S (S < S′), we can calculate the value f= S/S′, which is the fraction of available minimizers that the user will be able to hold in their database.
2. A minimum allowable hash value of v = (1 − f)∙M can also be calculated, where M is the maximum value output by hash function h.
3. Any minimizer in the reference library with a hash code less than v will not be inserted into the hash table.
4. This value v is also provided to the classifier so that only minimizers with hash codes greater than or equal to v will be used to probe the hash table, saving the search failure runtime penalty that would be incurred by searching for minimizers guaranteed not to be in the hash table.”

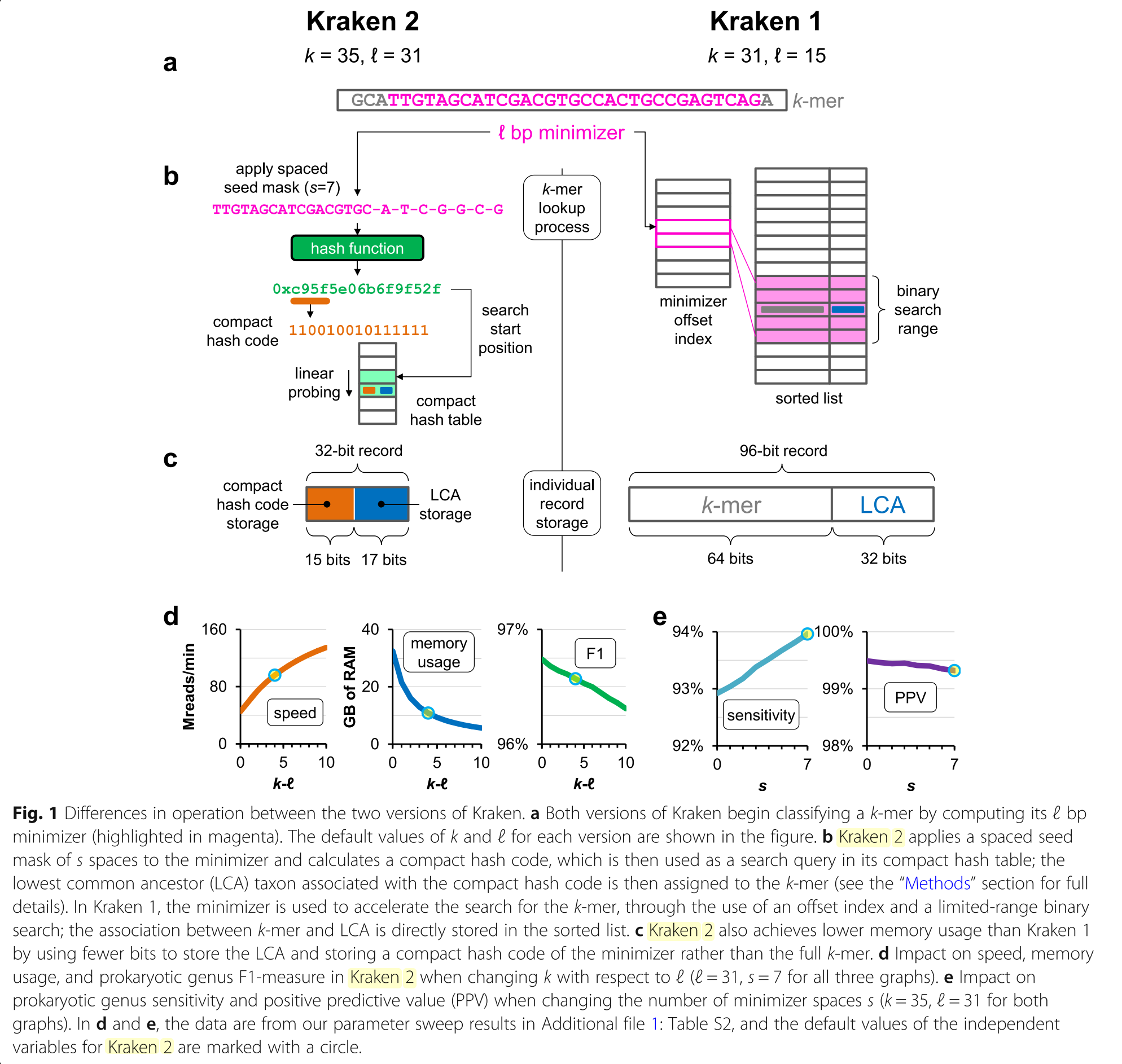
The defaults are \(k=35\) and \(l=31\).

Evaluating Performance of Classifier

• True- positive (TP)
• False-negative (FN)
• Vague positive (VP)
  • VP classification as a classification at an ancestor of the true genus of origin.
• False-positive (FP)

Sensitivity \(S=\frac{TP}{TP + VP + FN + FP}\) Positive Predictive Value (PPV) \(PPV=\frac{TP}{TP + FP}\) F1-measure (Harmonic mean of S and PPV)

• For 2D, harmonic mean is biased towards the lower of the two values. \(\left(\frac{1}{S}+\frac{1}{PPV}\right)^{-1}\)

Generally, a larger \(l\) value leads to larger compute time, larger database size and better accuracy. For \(S=35\), \(l={25 \rightarrow 31}\), database size increase from ~5Gb to ~10Gb, time of classification increase from 24s to 30s.

• Kraken 2 parameter vs performance supp
• Kraken 2 Manual

Bracken

To calculate abundance, Kraken 1/2 should be combined with Bracken. “Bracken (Bayesian Reestimation of Abundance with KrakEN) is a highly accurate statistical method that computes the abundance of species in DNA sequences from a metagenomics sample.”

Minimizers

The following excerpts are from this link.

“Only minimizers of the k-mers in the query sequences are used as database queries. Similarly, only minimizers of the k-mers in the reference sequences in the database’s genomic library are stored in the database. We will also refer to the minimizers as ℓ-mers, where ℓ ≤ k. All k-mers are considered to have the same LCA as their minimizer’s database LCA value.”

“Not all letters (digits) in Figure 2 are contained in minimizers: positions 1–3, 7, and 12 are not covered. Although it may not be required for every letter to be covered by a minimizer, it may be desirable for some applications. Gaps between minimizers are caused when the minimizers of two adjacent k-mers are more than L positions apart, as in the case of the k-mers starting in positions 4 and 5 in Figure 2: the minimizer of the k-mers in position 4 covers positions 4–6, while the minimizer for the next K-mer covers positions 8–10, leaving position 7 covered by no minimizer. However, note that the minimizers of two adjacent k-mers of size W can differ in their starting positions by at most W. Thus, gaps can be at most w − ℓ in size, so setting w ≤ ℓ ensures no gaps occur between minimizers. Then, all letters are covered except at most w − 1 at each end of the string”

In other words, to guarantee that there are no gaps, ensure that:

\[\begin{align} w &\le l \\ k &= w+l-1 \\ k &\le 2l-1 \\ &\approx 2l \end{align}\]

Refer to this tutorial on minimizer for a layman explanation. The code below is a rough example of how to identify minimizers of k-mers in a read.

# Sequence aka read
seq="ATGCGATATCGTAGGCGTCGATGGAGAGCTAGATCGATCGATCTAAATCCCGATCGATTCCGAGCGCGATCAAAGCGCGATAGGCTAGCTAAAGCTAGCA"
#reverse
rev=seq[::-1]
# A->T, T->A
rev=rev.replace("A","X")
rev=rev.replace("T","A")
rev=rev.replace("X","T")
# G->C, C->G
rev=rev.replace("C","X")
rev=rev.replace("G","C")
rev=rev.replace("X","G")

Kmer=31
M=7
L=len(seq)

# Iterate through k-mers of sequence
for i in range(0, L-Kmer+1):
        sub_f=seq[i:i+Kmer] # forward K-mer
        sub_r=rev[L-Kmer-i:L-i] # reverse and A-T,C-G swapped K-mer

        min="ZZZZZZZZZZZZZ"
        # Iterate through l-mers of k-mers, look for minimizer
        for j in range(0, Kmer-M+1):
                # look for minimizer
                sub2=sub_f[j:j+M]
                if sub2 < min:
                        min=sub2
                sub2=sub_r[j:j+M]
                if sub2 < min:
                        min=sub2

        print sub_f,min